![]()
Using congruence to establish properties of parallelograms
Theorem
The opposite sides of a parallelogram are equal.
Proof
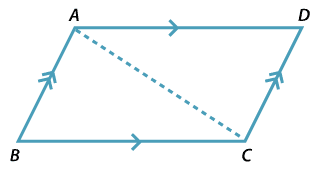
\(ABCD\) is a parallelogram.
To prove that \(AB = CD \ \text{and} \ AD = BC\), join
the diagonal \(AC\)
in the triangles \(ABC \ \text{and} \ CDA\).
| \(\angle BAC\) | = \(\angle DCA\) | (alternate angles, \(AB \| DC\)) | |
| \(\angle BCA\) | = \(\angle DAC\) | (alternate angles, \(AD \| BC\)) | |
| \(AC\) | = \(CA\) | (common) | |
| So \(\triangle ABC \equiv \triangle CDA\) (AAS) | |||
| Hence AB = CD and BC = AD | (matching sides of congruent triangles). | ||




